Abstract

polymeric resins are micro-molecules that by increasing the temperature (for overcoming the activation energy) begin to form covalent bonds and finally create a structure of thermoset block. Curing reactions rate increase by increasing of system temperature based on Arrhenius function. curing reaction of polymeric resin are exothermic. This means that by increasing the degree of reaction progress, accumulated heat increases the temperature of the system. Thus, with the progress of curing reactions, the released heat increases the temperature of the system and increases the curing rate. So, the temperature of curing systems of polymeric resin is not constant and it is needed to predict and control these changes with the help of computer simulation. In this article, MeasSoft has investigated the curing behavior and temperature changes of a type of polymeric resin in a cylindrical mold.

Keywords: Differential Scanning Calorimetry (DSC), SPI Test, Curing kinetics, Simulation, Heat, Temperature

Introduction

In the previous article (Thermal Kinetics of Polymers. Part I: Kinetic Parameters), the kinetics of curing of polymer resins were explained (please, read it). In this article, we want to Study the simulation of the curing system in cylindrical geometry.

Assuming that Some polymer resin at room temperature is poured into a cylindrical mold. Then, the mold is placed in an oil bath at a constant high temperature. The heat of the oil bath triggers the curing reactions and the temperature of sample rises due to the released curing heat. Due to differences in sample temperature and oil temperature (Thermal gradient), Heat transfer from the oil to resin raises the sample temperature. Over time, by starting of reaction, the direction of heat transfer is reversed until the heat of exothermic reaction is removed from the system. During test, all sample temperature changes is recorded by a thermocouple placed in the sample center. Using this test, the curing time, average of curing rate and maximum product temperature is recorded. It is clear that the reaction when ended that sample temperature changes became zero and curing system reached to steady state.

In this article, we want to study These events by mathematical simulation.

Theory: Mechanisms of Curing Kinetics

Two quite distinct mechanisms control thermal kinetics of curing systems:

1- Conductive heat transfer kinetics that controls the rate of heat transfer from the system to the environment and vice versa.

2- Curing reaction kinetics that controls the rate of heat production.

Heat curing kinetics of the system can be had two boundaries:

1- The system is completely isolated and adiabatic and no heat exchange occurs. Under this condition, the system reaches to maximum temperature and the product may reach to the degradation temperature. This system is created when the heat transfer coefficient is zero or the system dimensions are infinite .

2- The heat reaction comes out from the system as soon as it is produced. Under this condition, the heat reaction has no effect on the reaction because it is removed from the system as soon as it is produced. This system is created when the heat transfer coefficient is infinite or the system dimensions are almost zero .

So, theatrically, the curing system design should balance and optimize between Heat removal kinetics and Heat generation kinetics so that reaction energy wasting and damaging temperature elevation does not occur.

Process parameters of curing systems

1- Heat removal kinetics

One-dimensional Kinetics equation of conductive heat transfer obeys Fourier's law as follow: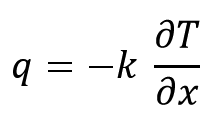

With regard to the equation, heat transfer kinetics is only a function of material type and Thermal gradient. Material type is a design parameter and temperature is a process parameter. Therefore temperature is only process parameter of heat removal kinetics.

2- Heat generation kinetics

Curing kinetics of thermosetting resins obeys the following equation: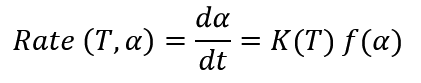

Where K is temperature function and f is conversion function (More details about this equation are given in the article of "Thermal Kinetics of Polymers. Part I: Kinetic Parameters"). The above equation indicates that temperature is only process parameter of Heat generation control.

Therefore, it is important to control the reaction heat kinetics and heat transfer kinetics and to select a suitable curing temperature.

Simulation

The differential equation of energy conservation law is shown in the following: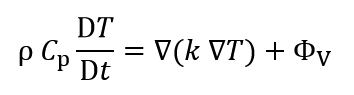

Where ρ, Cp, T, t, k and Φv are density, heat capacity, temperature, time, conductive heat transfer coefficient and reaction heat per unit volume, respectively.
It is reported that conductive heat transfer coefficient is a function of temperature as first-degree equation and its equation for polymers as follow [2]: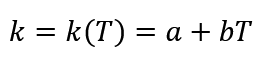

The amount of “bT” is an impressive amount at very high temperatures and in this study that “T” is less than 300°C (Safe temperature), “bT” can be ignored. So “k” can be considered constant: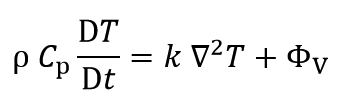

By expanding the above phrase at cylindrical coordinates the equation can be rewritten as: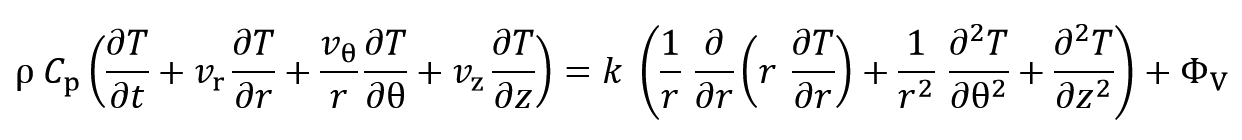

Where r, z and θ are radius, length and angle, respectively and vr, vz, vθ are velocity at r, z and θ directions. Since system boundaries are closed and material doesn’t flow or diffuse, so the system is dynamically static and velocity parameters are zero: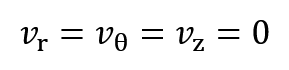

At the θ direction, there is no thermal gradient and at the z direction, heat transfer is ignored because of high length to radius ratio of sample: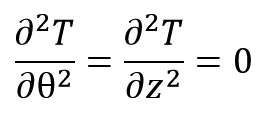

Thus, Equation 3 can be written as follows: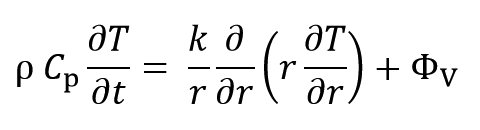

Thermal diffusion factor (λ) is defined as follows: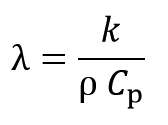
Φv is shown by the following equation:

The rate of reaction according to the previous work is given below: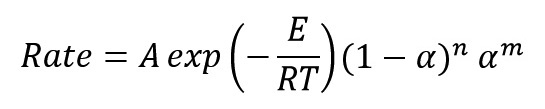

Boundary conditions are as follows:

1- central symmetry: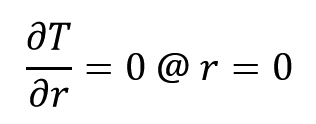

2- constant wall temperature:

Where T∞ is oil bath temperature.

 "MeasSoft Curing Simulation" is a simple software from MeasSoft that solves this differential equation and provides simulation results (you can get mor information about the software by contacting us by This email address is being protected from spambots. You need JavaScript enabled to view it.).

In the following, the simulation of curing system of a type of phenolic resin is provided.

Gel Time

Gel Time is he time required for changing of resin from a flowing liquid to a gel-like bulk. By considering conversion of reactions about 30% we can get this time from the software.

Result and Discussion

Phenolic Resin Data

The physical properties and thermal parameters of a type of phenolic resin required in the modeling are given at the Software table. All units are in SI system:

(The thermal parameters of the resin were calculated by DSC data and by using "MeasSoft Thermal Kinetics" Software)

In the following, simulation results of curing of benzoxazine in cylindrical coordinates by changing of two parameters of curing temperature and sample dimensions were offered and discussed.

First, curing of three different samples with a diameter of 10 mm at temperatures of 150, 170, 190°C and second, curing of three different samples with diameters of 10, 15 and 20 mm at temperature of 150°C were compared.

Curing simulation at different temperatures

The results of temperature changes with time of center of the resin in cylindrical system with diameter of 15 mm and at curing temperatures of 140, 160 and 180 °C were shown in the following figure.

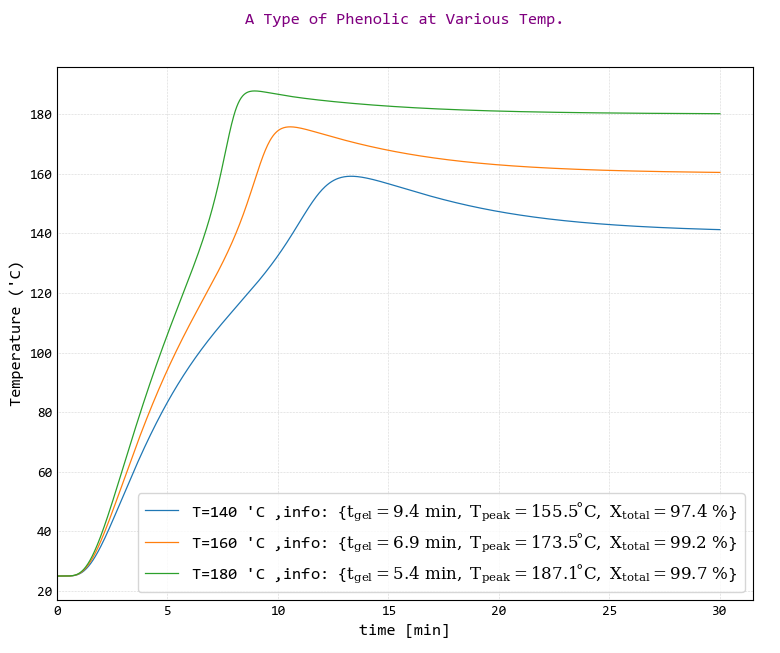
According to the figure, increasing the curing temperature increases the reaction rate and increasing reaction rate causes curing reaction start earlier and gel time occurs earlier and as wells the reaction end earlier. Consequently, it is meant to shortening curing time or narrowing of the peak width. Full curing of the resin means full releasing of curing heat thus the narrowing of the peak width and full releasing of curing heat causes peak height or maximum temperature (Tp) increase. In addition, according to the figure, increasing at curing temperature causes a product with a higher degree of conversion reaction was obtained.

Curing simulation at different dimensions

The results of temperature changes with time of the resin in cylindrical system with diameters of 15, 20 and 25 mm and at curing temperatures of 160 °C were shown in the following figure.

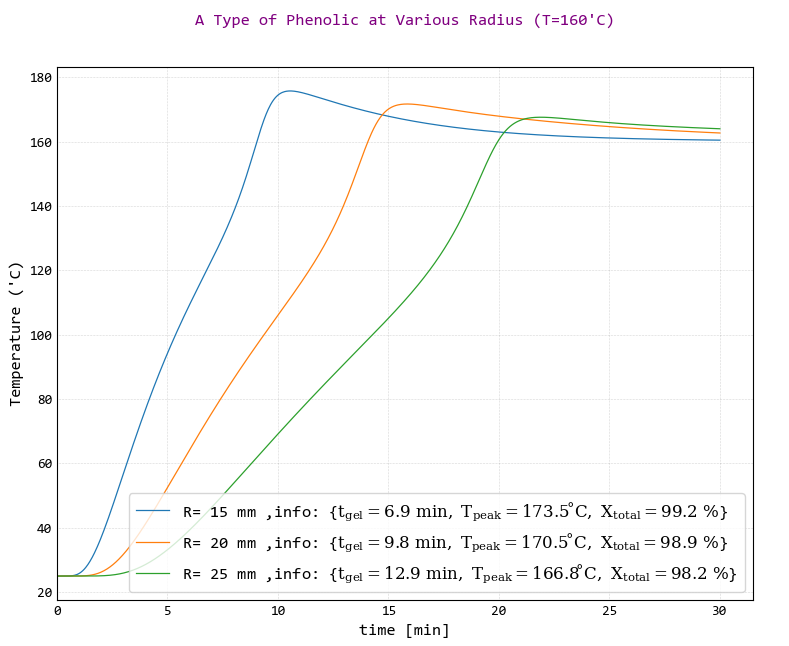
According to the figure, it is clear that increasing the curing system size causes the time of heat transfer be longer. This means rate of temperature variations or temperature-time slope reduced. Increasing of the time of heat transfer causes curing reaction start later that means longer gel time and decreasing of peak Temperature and decreasing final conversion.

Curing simulation by changing thermal conductivty

We added a kind of conductive nanoparticle to this resin. This nanoparticle has increased the thermal conductivity (k) of the final material. Four different samples were obtained by adding four different weight percent of these nanoparticles. In the following figure, The effect of increasing of the thermal conductivity is observed in the curing system.

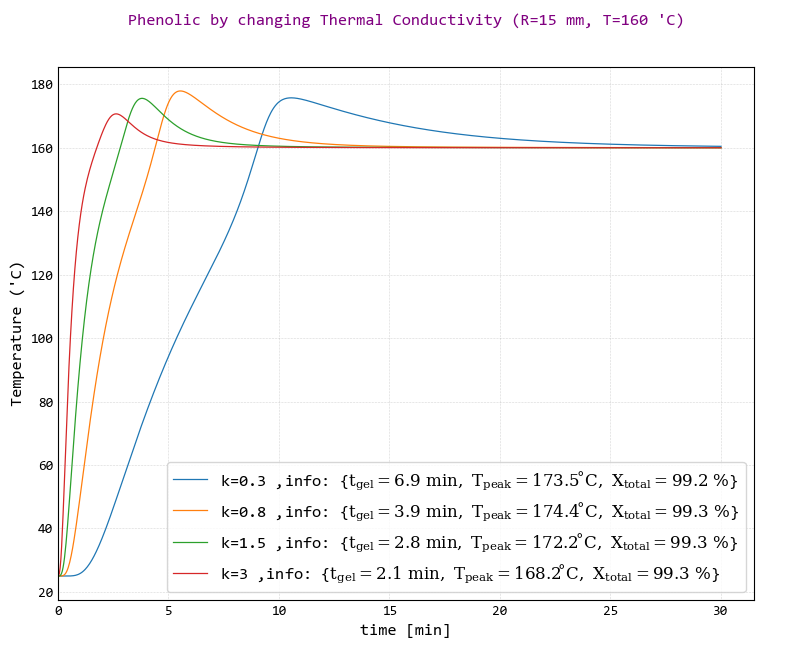
According to the picture, increasing of thermal conductivity causes decreasing of gel time, peak Temperature and slope of diagram.

Therefore, it can be said generally that increasing the thermal conductivity improves the curing system.